Maximum Rectangular Area in a Histogram

PROBLEM :

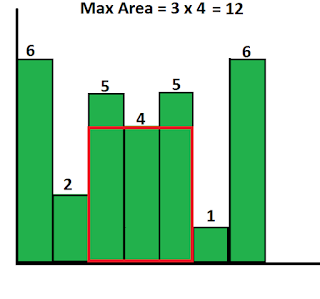
Find the largest rectangular area possible in a given histogram where the largest rectangle can be made of a number of contiguous bars. For simplicity, assume that all bars have same width and the width is 1 unit.

Input:
The first line contains an integer 'T' denoting the total number of test cases. In each test cases, the first line contains an integer 'N' denoting the size of array. The second line contains N space-separated integers A1, A2, ..., AN denoting the elements of the array. The elements of the array represents the height of the bars.


Output:
In each seperate line the maximum rectangular area possible from the contigous bars.


Constraints:
1<=T<=30
1<=N<=100
1<=A[i]<=1000


Example:
Input:
1
7
6 2 5 4 5 1 6

Output:
12

--------------------------------------------------------------------------------
SIMPLE c++ IMPLEMENTATION :(Using Auxilary arry)
--------------------------------------------------------------------------------

#include<iostream>
using namespace std ;
int Histogram(int [],int ) ;
int main()
{
int t,no,arr[100],i ;
cin>>t ;
while(t--)
{
cin>>no ;
for(i=0;i<no;i++)
cin>>arr[i] ;

no=Histogram(arr,no) ;
cout<<no<<endl ;
}
return 0 ;
}

int Histogram(int arr[],int no)
{
int i,top,t,area,max ;
int stack[no] ;
top=-1 ;
max=0 ;
i=0 ;

while(i<no)
{
if(top==-1||arr[stack[top]]<=arr[i])
stack[++top]=i++ ;
else
{
t=stack[top] ;
top-- ;

if(top==-1)
area=arr[t]*i ;
else
area=arr[t]*(i-stack[top]-1) ;

if(max<area)
max=area ;
}
}

while(top!=-1)
{
t=stack[top] ;
top-- ;

if(top==-1)
area=arr[t]*i ;
else
area=arr[t]*(i-stack[top]-1) ;

if(max<area)
max=area ;
}
return max ;
}

---------------------------------------------------------------------------------