CSE Company Interview Questions

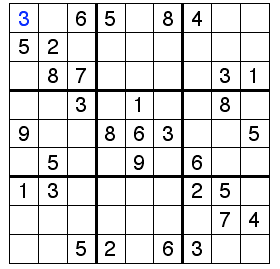
PROBLEM : Given an incomplete Sudoku configuration in terms of a 9x9  2-D square matrix (mat[][]) the task to print a solution of the Sudoku. For simplicity you may assume that there will be only one unique solution. Example For the above configuration the solution is 3 1 6 5 7 8 4 9 2 5 2 9 1 3 4 7 6 8 4 8 7 6 2 9 5 3 1 2 6 3 4 1 5 9 8 7 9 7 4 8 6 3 1 2 5 8 5 1 7 9 2 6 4 3 1 3 8 9 4 7 2 5 6 6 9 2 3 5 1 8 7 4 7 4 5 2 8 6 3 1 9 Input: The first line of input contains an integer T denoting the no of test cases. Then T test cases follow. Each test case contains 9*9 space separated values of the matrix mat[][] representing an incomplete Sudoku state where a 0 represents empty block. Output: For each test case in a new line print the space separated values of the solution of the the sudoku. Constraints: 1<=T<=10 0<=mat[]<=9 Example: Input: 1 3 0 6 5 0 8 4 0 0 5 2 0 0 0 0 0 0 0 0 8 7 0 0 0 0 3 1 0 0 3 0 1 0 0 8 0 9 0 0 8 6 3 0 0 5 0 5 0 0 ...

PROBLEM : The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other. Given an integer n, print all distinct solutions to the n-queens puzzle. Each solution contains distinct board configurations of the n-queens’ placement, where the solutions are a permutation of [1,2,3..n] in increasing order, here the number in the ith place denotes that the ith-column queen is placed in the row with that number. For eg below figure represents a chessboard [3 1 4 2]. Input: The first line of input contains an integer T denoting the no of test cases. Then T test cases follow. Each test case contains an integer n denoting the size of the chessboard. Output: For each test case, output your solutions on one line where each solution is enclosed in square brackets '[', ']' separated by a space . The solutions are permutations of {1, 2, 3 …, n} in increasing order where the number in the ith place denotes the ith-co...

PROBLEM : Consider a rat placed at (0, 0) in a square matrix m[][] of order n and has to reach the destination at (n-1, n-1). Your task is to complete the function which returns a sorted array of strings denoting all the possible directions which the rat can take to reach the destination at (n-1, n-1). The directions in which the rat can move are 'U'(up), 'D'(down), 'L' (left), 'R' (right). For example 1 0 0 0 1 1 0 1 1 1 0 0 0 1 1 1 For the above matrix the rat can reach the destination at (3, 3) from (0, 0) by two paths ie DRDDRR and DDRDRR when printed in sorted order we get DDRDRR DRDDRR. Input: The first line of input contains an integer T denoting the no of test cases. Then T test cases follow. Each test case contains two lines. The first line contains an integer n denoting the size of the square matrix. The next line contains n*n space separated values of the matrix m where 0's represents blocked paths and 1 represent valid path...