Solve the Sudoku

PROBLEM :

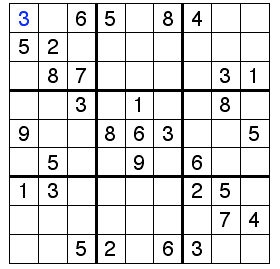
Given an incomplete Sudoku configuration in terms of a 9x9  2-D square matrix (mat[][]) the task to print a solution of the Sudoku. For simplicity you may assume that there will be only one unique solution.

Example



For the above configuration the solution is
3 1 6 5 7 8 4 9 2
5 2 9 1 3 4 7 6 8
4 8 7 6 2 9 5 3 1
2 6 3 4 1 5 9 8 7
9 7 4 8 6 3 1 2 5
8 5 1 7 9 2 6 4 3
1 3 8 9 4 7 2 5 6
6 9 2 3 5 1 8 7 4
7 4 5 2 8 6 3 1 9


Input:
The first line of input contains an integer T denoting the no of test cases. Then T test cases follow. Each test case contains 9*9 space separated values of the matrix mat[][] representing an incomplete Sudoku state where a 0 represents empty block.

Output:
For each test case in a new line print the space separated values of the solution of the the sudoku.

Constraints:
1<=T<=10
0<=mat[]<=9

Example:
Input:
1
3 0 6 5 0 8 4 0 0 5 2 0 0 0 0 0 0 0 0 8 7 0 0 0 0 3 1 0 0 3 0 1 0 0 8 0 9 0 0 8 6 3 0 0 5 0 5 0 0 9 0 6 0 0 1 3 0 0 0 0 2 5 0 0 0 0 0 0 0 0 7 4 0 0 5 2 0 6 3 0 0

Output:
3 1 6 5 7 8 4 9 2 5 2 9 1 3 4 7 6 8 4 8 7 6 2 9 5 3 1 2 6 3 4 1 5 9 8 7 9 7 4 8 6 3 1 2 5 8 5 1 7 9 2 6 4 3 1 3 8 9 4 7 2 5 6 6 9 2 3 5 1 8 7 4 7 4 5 2 8 6 3 1 9
       
--------------------------------------------------------------------------------
SIMPLE c++ IMPLEMENTATION :
--------------------------------------------------------------------------------

#include<iostream>
using namespace std;
#define N 9

bool FindSpace(int chess[N][N],int *row,int *col)
{
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
            if(!chess[i][j])
            {
                (*row)=i ;
                (*col)=j ;
                return false ;
            }
    return true ;
}

bool IsSafe(int chess[N][N],int row,int col,int no)
{
    for(int i=0;i<N;i++)
        if(chess[row][i]==no)
            return false ;
           
    for(int i=0;i<N;i++)
        if(chess[i][col]==no)
            return false ;
           
    row=row-(row%3) ;
    col=col-(col%3) ;
   
    for(int i=0;i<3;i++)
        for(int j=0;j<3;j++)
            if(chess[i+row][j+col]==no)
                return false ;
               
    return true ;
}

bool SolveSudoku(int chess[N][N])
{
    int row,col ;
   
    if(FindSpace(chess,&row,&col))
        return true ;
       
    for(int i=1;i<=9;i++)
    {
        if(IsSafe(chess,row,col,i))
        {
            chess[row][col]=i ;
           
            if(SolveSudoku(chess))
                return true ;
               
            chess[row][col]=0 ;
        }
    }
   
    return false ;
}

int main()
{
int t ;
cin>>t ;
while(t--)
{
   int chess[N][N] ;
 
   for(int i=0;i<N;i++)
       for(int j=0;j<N;j++)
           cin>>chess[i][j] ;
         
        if(SolveSudoku(chess))
        {
            for(int i=0;i<N;i++)
           for(int j=0;j<N;j++)
               cout<<chess[i][j]<<" " ;
        }
        else
            cout<<"No solution exists" ;
        cout<<endl ;
}
return 0;
}

--------------------------------------------------------------------------------

Comments

Post a Comment

Popular posts from this blog

Count ways to N'th Stair(Order does not matter)

PROBLEM : There are n stairs, a person standing at the bottom wants to reach the top. The person can climb either 1 stair or 2 stairs at a time. Count the number of ways, the person can reach the top (order does not matter). Order does not matter means for n=4 {1 2 1},{2 1 1},{1 1 2} are considered same. Input: The first line contains an integer 'T' denoting the total number of test cases. In each test cases, an integer N will be given. Output: Print number of possible ways to reach Nth stair. Constraints: 1<=T<=1000 1<=N<=100 Example: Input: 1 4 Output: 3 -------------------------------------------------------------------------------- SIMPLE c++ IMPLEMENTATION : -------------------------------------------------------------------------------- #include<iostream> using namespace std; long long Count_nth_stair(long long ) ; int main()  { int t ; long long no ; cin>>t ; while(t--) {    cin>>no ; ...
Read more

Replace all ‘0’ with ‘5’ in an input Integer

PROBLEM : Given a number your task is to complete the function convertFive which takes an integer n as argument and replaces all zeros in the number n with 5 .Your function should return the converted number . Input: The first line of input contains an integer T denoting the number of test cases . Then T test cases follow . Each test case contains a single integer n denoting the number. Output: The output of the function will be an integer where all zero's are converted to 5 . Constraints: 1<=T<100 1<=n<=10000 Example: Input 2 1004 121 Ouput 1554 121 -------------------------------------------------------------------------------- SIMPLE c++ IMPLEMENTATION : -------------------------------------------------------------------------------- /*you are required to complete this method*/ int convertFive(int n) {     int k,r ;     k=0 ;         while(n!=0)     {         r=n%10...
Read more

Chocolate Distribution Problem

PROBLEM : Given an array A[] of N integers where each value represents number of chocolates in a packet. Each packet can have variable number of chocolates. There are m students, the task is to distribute chocolate packets such that : 1. Each student gets one packet. 2. The difference between the number of chocolates given to the students in packet with maximum chocolates and packet with minimum chocolates is minimum. Examples Input : A[] = {3, 4, 1, 9, 56, 7, 9, 12}         m = 5 Output: Minimum Difference is 6 We may pick 3,4,7,9,9 and the output is 9-3 = 6 Input : A[] = {7, 3, 2, 4, 9, 12, 56}         m = 3 Output: Minimum difference is 2 We can pick 2, 3 and 4 and get the minimum difference between maximum and minimum packet sizes. ie 4-2 = 2 Input: The first line of input contains an integer T, denoting the no of test cases. Then T test cases follow. Each test case consists of three lines. The first line of each test ca...
Read more

Remove characters from the first string which are present in the second string

PROBLEM : Given two strings s1 & s2, remove those characters from first string which are present in second string. Both the strings are different and contain only lowercase characters. Input: The first line of input contains an integer T denoting the number of test cases. The first line of each test case is s1,s1 is first string. The second line of each test case contains s2,s2 is second string. Output: Print the modified string(s1). For each test case, print the output in a new line. Constraints: 1 = T = 15 1 = s2 < s1 = 50 Example: Input: 2 geeksforgeeks mask removeccharaterfrom string Output: geeforgee emovecchaaefom -------------------------------------------------------------------------------- SIMPLE c++ IMPLEMENTATION : -------------------------------------------------------------------------------- #include<iostream> using namespace std; #include<stdlib.h> void Remove_character(char *,char *) ; int main()  { ...
Read more

Primality Test ( CodeChef Problem code: PRB01 )

PROBLEM : Alice and Bob are meeting after a long time. As usual they love to play some math games. This times Alice takes the call and decides the game. The game is very simple, Alice says out an integer and Bob has to say whether the number is prime or not. Bob as usual knows the logic but since Alice doesn't give Bob much time to think, so Bob decides to write a computer program. Help Bob accomplish this task by writing a computer program which will calculate whether the number is prime or not . Input The first line of the input contains T testcases, T lines follow Each of T line contains an integer N which has to be tested for primality Output For each test case output in a separate line, "yes" if the number is prime else "no" Constraints 1<=T<=20 1<=N<=10000 1<=M<=10000 Input: 5 23 13 20 1000 99991 Output: yes yes no no yes       --------------------------------------------------------------------------...
Read more